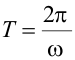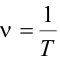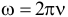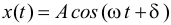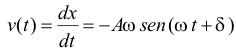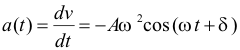Sistema Diédrico

De vuelta de unos días estivales de descanso, he decidido ponerme con uno de los temas fundamentales del Sistema Diédrico: la perpendicularidad. Es muy importante porque será útil, entre otros, para las distancias y las alturas de poliedros regulares. La perpendicularidad ya la pusimos en práctica en este problema de las PAU para dibujar una Pirámide en Sistema Diédrico.

No pierdas detalle. Te explicaré por separado los 4 casos de perpendicularidad posibles con la mayor claridad. Verás como te resulta sencillo.

1. Recta perpendicular a plano

Una recta es perpendicular a un plano cuando sus proyecciones son perpendiculares a las trazas del plano.

Para dibujar una recta perpendicular a un plano dado por un punto, simplemente tendremos que dibujar sus proyecciones perpendiculares a las trazas del plano pasando por el punto.

Excepción: Planos paralelos a la Línea de Tierra y planos que contienen a la Línea de Tierra. En ambos casos, la recta perpendicular es una Recta de Perfil. Para ver la perpendicularidad necesitaremos un plano auxiliar de perfil.

2. Rectas perpendiculares entre sí

Dos rectas perpendiculares en el espacio, en general, no tienen sus proyecciones perpendiculares. Únicamente cuando una de las rectas es paralela a uno de los planos de proyección, las proyecciones de ambas rectas sobre este plano serán perpendiculares.

Esto quiere decir que, para dos rectas perpendiculares en el espacio:

• Si una es horizontal, sus proyecciones horizontales son perpendiculares
• Si una es frontal, sus proyecciones verticales son perpendiculares

Una recta es perpendicular a otra cuando está contenida en un plano perpendicular a dicha recta. Una recta es perpendicular a un plano cuando sus proyecciones son perpendiculares a las trazas del plano.

De aquí se deduce que un plano perpendicular a la recta contiene las infinitas rectas perpendiculares a dicha recta.

Recta perpendicular a otra por un punto

Para dibujar una recta perpendicular a otra dada por un punto existen 2 posibilidades:

1. Dibujar una recta horizontal o frontal que tenga sus proyecciones horizontales o verticales respectivamente perpendiculares a la dada y que pase por el punto.
2. Dibujar un plano perpendicular a la recta dada que pase por el punto y en él contener una recta. Esto lo veremos en el siguiente apartado.

3. Plano perpendicular a recta

Un plano es perpendicular a una recta cuando sus trazas son perpendiculares a las proyecciones de la recta (igual que hemos visto en el apartado 1)

Excepción: Rectas de Perfil. Para dibujar un plano perpendicular a una recta de perfil tendremos que utilizar un plano auxiliar de perfil.

Plano perpendicular a recta por un punto

Para dibujar un plano perpendicular a una recta por un punto dado utilizaremos una recta auxiliar que sea perpendicular a la dada y pase por el punto. Por sus puntos traza dibujaremos el plano perpendicular.

Ejemplo: Dibujar el plano P’-P perpendicular a la recta dada r’-r y que pase por el punto a’-a.

1. Dibuja la proyección horizontal de la recta s’-s que pase por a y sea perpendicular a la proyección horizontal r de la recta.
2. Dibuja proyección vertical s’ de la recta, que pase por a’ y sea paralela a la Línea de Tierra.
3. Obtén el punto traza vertical de dicha recta s’-s.
4. Pasa la traza vertical P’ del plano perpendicular a la proyección vertical r’ de la recta
5. Por el punto de corte de P’ con la Línea de Tierra dibuja la traza horizontal P del plano perpendicular a la proyección horizontal r de la recta.

4. Planos perpendiculares entre sí

Dos planos son perpendiculares entre sí cuando uno de ellos contiene una recta perpendicular al otro.

Se deduce de aquí que:

• Sus trazas no tienen que ser necesariamente perpendiculares.
• Dado un plano, los infinitos planos que contienen a una recta perpendicular al dado serán perpendiculares a este.

Plano perpendicular a otro por un punto

Dado un plano P’-P y un punto a’-a, dibujar otro plano Q’-Q perpendicular al dado.

1. Dibuja una recta r’-r perpendicular a P’-P que pase por a’-a y halla sus puntos traza.
2. Dibuja cualquier plano que contenga a la recta r’-r, es decir, cuyas trazas pasen por los puntos traza de la recta.

Como puedes comprobar, este ejercicio tiene infinitas soluciones.

Plano perpendicular a otros dos por un punto

Dados los planos P’-P y Q’-Q y un punto a’-a, dibujar otro plano J’-J perpendicular a los 2 dados.

1. Dibuja una recta r’-r perpendicular a P’-P que pase por a’-a y halla sus puntos traza.
2. Dibuja una recta s’-s perpendicular a Q’-Q que pase por a’-a y halla sus puntos traza (basta con encontrar 3 puntos traza de ambas rectas)
3. Dibuja el plano que contiene ambas rectas r’-r y s’-s, es decir, cuyas trazas pasan por los puntos traza de ambas rectas.

Este ejercicio tiene una única solución.

Resumen

Básicamente te he explicado todos los casos de perpendicularidad posibles junto con sus excepciones. Los casos concretos se presentarán en ejercicios concretos, pero, en esencia has aprendido los conceptos generales que te permitirán deducir la solución a cualquier ejercicio.

Fuente: https://www.10endibujo.com/perpendicularidad-diedrico/

Poesía arraigada y desarraigada

La poesía en España durante los años 40.

En la inmediata posguerra se abrieron varias vías para la poesía. Vamos a estudiar las dos que tuvieron mayor relevancia: la poesía arraigada y desarraigada. El protagonismo poético de estos años se lo llevan los representantes de estos dos grupos con propuestas totalmente distintas.

• Por un lado estarían los autores que se identifican con el régimen franquista. Ofrecen una visión idealizada y heroica de la vida que no se corresponde con la realidad de España en esos años. Defienden además los valores del régimen: familia patriarcal y moral católica. Practican una poesía que Dámaso Alonso catalogó de arraigada.

• Mientras que el otro grupo, no se identifican con la nueva España resultado de la guerra y ven en el ser humano las consecuencias de la barbarie, la destrucción y el reflejo del dolor existencial. Estos representan la nueva poesía desarraigada.

1.1. Rasgos de la poesía arraigada y desarraigada

A) Poesía arraigada

Representada por un grupo de autores que ofrecen una visión idealizada y entusiasta del mundo. La poesía no refleja la verdadera situación de España tras la guerra, sino que busca la evasión refugiándose en temas como el amor, la belleza de Dios y la creación. Defienden, en definitiva, los valores del bando franquista.

Se agruparon en torno a dos revistas, Escorial (1940) y mas tarde nacerá la revista Garcilaso. Precisamente por esta revista también fueron llamados garcilasistas, no fue solo un nombre. Practicar poesía garcilasista suponía una vuelta a la lírica de Garcilaso y otros poetas de la tradición renacentista.

Los rasgos formales de esta poesía son:

– Las formas estróficas preferidas son las clásicas: sonetos, tercetos,…

– Los  temas principales son los clásicos de la poesía de todos los tiempos: el amor, el  paisaje, las cosas bellas, etc.

– El tema de Dios como protector del hombre y fuente de la perfección y el orden del mundo.

– Ausencia de compromiso y distanciamiento de la realidad.

Destacan autores (que luego la mayoría de ellos sufrirá un desengaño de ese mundo idealizado), como Dionisio Ridruejo, Luis García Nieto, Leopoldo Panero o Luis Rosales. Éste último será muy influyente, e iniciará el giro posterior de estos poetas  hacia una poética más existencialista, con  su obra La casa encendida.
B) Poesía desarraigada

Esta corriente representa el primer movimiento de renovación estética después de la Guerra Civil. Contrariamente a los anteriores, para estos poetas el mundo es un caos y una angustia. Dámaso Alonso (poeta de la Generación del 27), con su libro Hijos de la ira (1944) será quien marque la línea de esta escuela, secundado por otro poeta del 27, Vicente Aleixandre con su obra Sombra del paraíso (1944).

Los poetas “desarraigados” se agruparon principalmente en la revista Espadaña, fundada por Victoriano Crémer y Eugenio de Nora.

Los rasgos de esta poesía son:

• En los temas, Dios sigue siendo uno de los motivos principales de las composiciones poéticas. Pero, a diferencia de  la poesía arraigada, su religiosidad es crítica. Transmite la idea de que Dios ha abandonado al ser humano y, en consecuencia, el mundo está dominado por  la soledad o vacío existencial y el miedo de vivir y de morir. Corresponde esta corriente a la tendencia existencialista que se generaliza en toda la literatura europea tras la Segunda Guerra Mundial

Estilísticamente, es una poesía menos clasicista que la anterior, con un lenguaje más directo y sencillo, donde no importa tanto la estructura del poema como el contenido. Sin embargo, esta sencillez formal es sólo aparente. En la métrica, emplean el verso libre, pero también  el soneto que predomina en la mayoría de las composiciones y otras estrofas populares.

Destacan autores como: Dámaso Alonso, Carlos Bousoño, José Luis Hidalgo, Leopoldo de Luis, Vicente Gaos, Gabriel Celaya, José Hierro  o Blas de Otero. La poesía de la mayoría de ellos evolucionará después hacia la poesía social.

Fuente: https://masterlengua.com/poesia-arraigada-y-desarraigada/

Movimiento harmónico simple

Empezamos el segundo trimestre con un tema un poco más complejo.

Un movimiento armónico simple es el que describe una partícula sometida a una fuerza restauradora proporcional a su desplazamiento. Se genera entonces un movimiento periódico, es decir que se repite cada cierto intervalo de tiempo. No todos los movimientos periódicos son armónicos. Para que lo sean, la fuerza restauradora debe ser proporcional al desplazamiento.

El problema del oscilador armónico simple aparece con mucha frecuencia en Física, ya que una masa en equilibrio bajo la acción de cualquier fuerza conservativa, en el límite de movimientos pequeños, se comporta como un oscilador armónico simple.

En la siguiente animación se muestra el movimiento de una masa sujeta a un muelle. Pinchando sobre ella y arrastrando se desplaza de su posición de equilibrio. Con el mando puedes variar su frecuencia de oscilación.

A continuación se explica el movimiento que describe la masa bajo la acción de la fuerza recuperadora del muelle.

La masa sujeta al muelle describe un movimiento oscilatorio. Para calcular su aceleración utilizamos la Segunda Ley de Newton:

Definimos la frecuencia angular ω como:

Sus unidades en el SI son rad/s.

Posición, velocidad y aceleración

Para calcular la posición de la masa en función del tiempo habría que resolver la ecuación diferencial anterior que relaciona la aceleración con el desplazamiento.

Sin embargo, para simplificar vamos a dar la solución. Derivándola dos veces se demuestra fácilmente que satisface la Segunda Ley de Newton.

La constante A que aparece en la expresión anterior se denomina amplitud del movimiento, y es el máximo desplazamiento de la masa con respecto a su posición de equilibrio x = 0. Sus unidades en el SI son los metros (m).

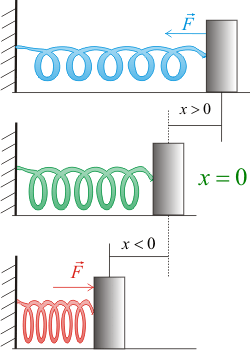
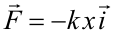
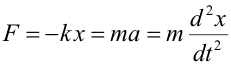
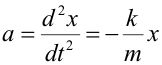
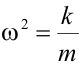
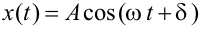
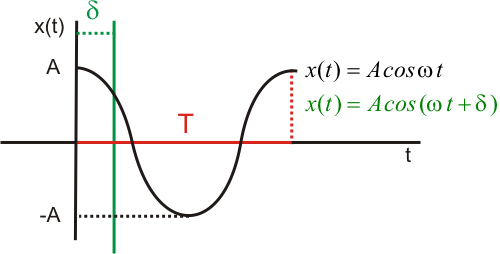
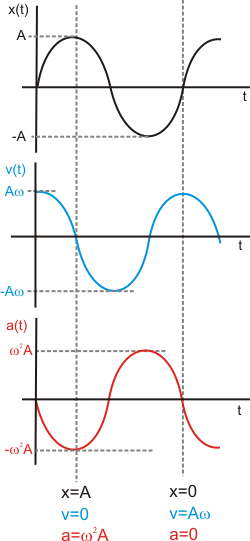
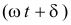El argumento del coseno es la fase y se mide en radianes.

δ es la constante de fase y viene determinada por las condiciones iniciales del problema.

El tiempo que tarda la masa en efectuar una oscilación completa se denomina periodo (T), y está relacionado con la frecuencia angular mediante la expresión:

El número de oscilaciones que se realiza en un segundo se llama frecuencia ν y se calcula como la inversa del periodo:

Se mide en s^-1 o Herzios (Hz)

De la definición de frecuencia se obtiene que 

La velocidad y la aceleración de una partícula que describe un movimiento armónico simple se obtiene derivando la ecuación de la posición en función del tiempo.

Energía

Si no existe rozamiento entre el suelo y la masa, la energía mecánica de esta última se conserva. Ya se vio en el apartado de trabajo que la fuerza recuperadora del muelle es una fuerza conservativa y se calculó su energía potencial asociada, que es una parábola:

En la siguiente figura se ha representado la energía total, la energía potencial elástica y la cinética para distintas posiciones de una partícula que describe un movimiento armónico simple.

La energía mecánica se conserva, por lo que para cualquier valor de x la suma de la energía cinética y potencial debe ser siempre:

Fuente: https://www2.montes.upm.es/dptos/digfa/cfisica/dinam1p/mas.html

Geometría analítica

¿Qué es la geometría analítica?

La geometría analítica es una rama de las matemáticas dedicada al estudio en profundidad de las figuras geométricas y sus respectivos datos, tales como áreas, distancias, volúmenes, puntos de intersección, ángulos de inclinación, etcétera. Para ello emplea técnicas básicas de análisis matemático y de álgebra

Utiliza un sistema de coordenadas conocido como el Plano cartesiano, que es bidimensional y está compuesto por dos ejes: uno de abscisas (eje x) y otro de ordenadas (eje y). Allí se pueden estudiar todas las figuras geométricas que sean de nuestro interés, asignando a cada punto de la misma un lugar puntual de coordenadas (x, y).

Así, los análisis de la geometría analítica usualmente comprenden la interpretación matemática de una figura geométrica, es decir, la formulación de ecuaciones. O bien puede ser lo contrario: la representación gráfica de una ecuación matemática. Esta equivalencia se encuentra plasmada en la fórmula y = f(x), donde f es una función de algún tipo.

La geometría analítica es un campo fundamental de las matemáticas que suele formar parte del pensum de estudios de la secundaria.

Historia de la geometría analítica

El fundador de este campo de estudio se considera el filósofo francés René Descartes (1596-1650), con el apéndice titulado “La Geometrie” en su célebre obra Discurso del método.

Sin embargo, en el siglo XI, el matemático persa Omar Khayyam (c.1048-c.1131) empleó ideas semejantes, que Descartes difícilmente podía conocer. Es decir que ambos probablemente las inventaron por cuenta propia.

Dado lo herméticas de las ideas de Descartes, el matemático holandés Franz van Schooten (1615-1660) y sus colaboradores ampliaron, desarrollaron y divulgaron la geometría analítica en Occidente. Solía llamársela “Geometría cartesiana”, para rendir homenaje a su creador, pero ese término hoy en día prefiere usarse para referirse únicamente al apéndice escrito por Descartes.

Aplicaciones de la geometría analítica

Los puentes colgantes pueden ser diseñados gracias a la geometría analítica.

La geometría analítica es una de las herramientas conceptuales más útiles de la humanidad, y hoy en día sus aplicaciones podemos verlas en, por citar unos ejemplos:

• Los puentes colgantes. Desde los antiguos puentes colgantes de madera, hasta sus versiones modernas con cables de acero, el principio geométrico de la parábola se aplica en cada uno de ellos.
• Las antenas parabólicas. Las antenas parabólicas para captar información satelital tienen la forma de un paraboloide, generado por su reflector que gira sobre el eje, persiguiendo la señal. Gracias a la propiedad de reflexión de la parábola, el disco de la antena puede reflejar la señal satelital hacia el dispositivo de alimentación.
• La observación astronómica. Los cuerpos celestes orbitan en una trayectoria que describe una elipse, como lo dedujo Johannes Kepler (1571-1630), y no una circunferencia, como creía Copérnico (1473-1543). Dichos cálculos fueron posibles sólo empleando la Geometría analítica.

Fórmulas de la geometría analítica

La geometría analítica ofrece fórmulas para las figuras geométricas.

La geometría estudia las figuras geométricas y obtiene sus ecuaciones básicas, como son:

• Las rectas se describen mediante la fórmula ax + by = c.
• Los círculos se describen mediante la fórmula x² + y² = 4.
• Las hipérbolas se describen mediante la fórmula xy = 1.
• Las parábolas se describen mediante la fórmula y = ax² + bx + c.
• Las elipses se describen mediante la fórmula (x²/a²) + (y²/b²) = 1.

Fuente: https://concepto.de/geometria-analitica/#ixzz8LrdpUHPJ